0.10 / 7.2 X 10-4
instantreferrals
Sep 03, 2025 · 5 min read
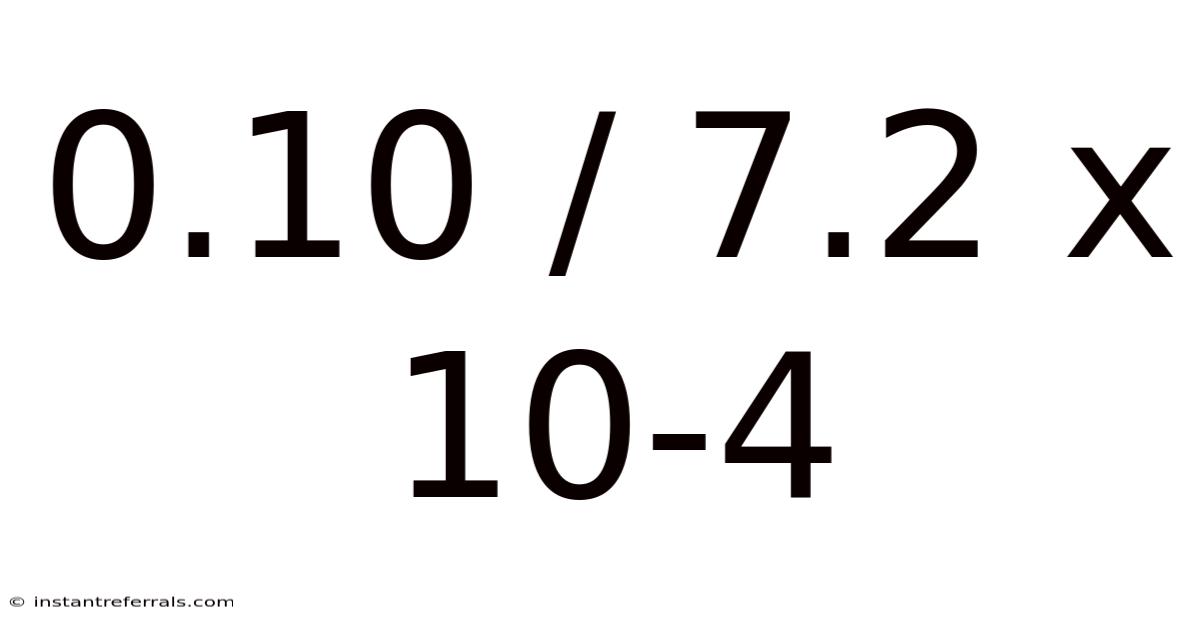
Table of Contents
Decoding 0.10 / 7.2 x 10⁻⁴: A Deep Dive into Scientific Notation and Calculations
This article explores the seemingly simple calculation of 0.10 / 7.2 x 10⁻⁴, unraveling the underlying principles of scientific notation and demonstrating a step-by-step approach to solving it. We'll delve into the significance of each element, clarify potential points of confusion, and provide a comprehensive understanding of the process involved. This guide is designed for anyone from high school students grappling with scientific notation to adults seeking to refresh their mathematical skills. Mastering this calculation will build a solid foundation for more complex scientific and engineering problems.
Understanding Scientific Notation
Before tackling the calculation, let's solidify our grasp of scientific notation. Scientific notation is a way of expressing numbers that are either very large or very small in a concise and manageable format. It follows the form:
a x 10ᵇ
Where:
- 'a' is a number between 1 and 10 (but not including 10). This is called the coefficient or mantissa.
- 'b' is an integer exponent representing the power of 10. A positive exponent indicates a large number, while a negative exponent indicates a small number.
For example:
- 6,000,000 can be written as 6 x 10⁶
- 0.0000045 can be written as 4.5 x 10⁻⁶
Breaking Down the Calculation: 0.10 / 7.2 x 10⁻⁴
Our target calculation is 0.10 / 7.2 x 10⁻⁴. This involves several steps:
Step 1: Converting to Scientific Notation
First, let's express all numbers in scientific notation. 0.10 becomes 1.0 x 10⁻¹. This makes the calculation:
(1.0 x 10⁻¹) / (7.2 x 10⁻⁴)
Step 2: Separating the Coefficients and Exponents
To simplify the calculation, let's separate the coefficients and the exponents:
(1.0 / 7.2) x (10⁻¹ / 10⁻⁴)
Step 3: Calculating the Coefficients
Now, we can calculate the division of the coefficients:
1.0 / 7.2 ≈ 0.13888...
We can express this in scientific notation as 1.3888... x 10⁻¹
Step 4: Calculating the Exponents
Next, we address the exponents. Remember the rule of exponents: aᵐ / aⁿ = aᵐ⁻ⁿ. Therefore:
10⁻¹ / 10⁻⁴ = 10⁻¹⁻⁽⁻⁴⁾ = 10⁻¹⁺⁴ = 10³
Step 5: Combining the Results
Finally, we combine the calculated coefficient and exponent to arrive at the final answer:
(1.3888... x 10⁻¹) x (10³) = 1.3888... x 10²
This is approximately equal to 138.89. Depending on the level of precision required, you may round the answer to a suitable number of significant figures. In this case, given the initial values, two significant figures are appropriate, yielding a final answer of 140.
A Deeper Dive into the Mathematical Principles
Let's examine the underlying mathematical concepts more closely. The calculation involves several key arithmetic operations:
-
Division: The primary operation is division, where we divide 0.10 by 7.2 x 10⁻⁴. Understanding the order of operations (PEMDAS/BODMAS) is crucial here. While multiplication and division are of equal precedence, we work from left to right.
-
Scientific Notation and Exponents: The effective use of scientific notation simplifies the handling of very small or very large numbers. The manipulation of exponents (adding or subtracting exponents in multiplication and division) is a fundamental aspect of working with scientific notation.
-
Significant Figures: The concept of significant figures is vital in scientific calculations. Significant figures reflect the precision of a measurement or calculation. Rounding to the appropriate number of significant figures ensures that the result accurately reflects the uncertainty inherent in the initial values.
Practical Applications and Real-World Examples
Calculations like 0.10 / 7.2 x 10⁻⁴ are not merely abstract exercises. They have numerous practical applications across various fields:
-
Chemistry: Calculations involving molarity, concentration, and stoichiometry frequently utilize scientific notation and these types of operations.
-
Physics: Many physical constants and measurements, especially in areas like quantum mechanics and astrophysics, are expressed in scientific notation.
-
Engineering: Engineering problems, from calculating the stress on a material to designing electronic circuits, involve calculations with very large or very small numbers.
-
Computer Science: In computer science, dealing with binary data and memory allocation often necessitates working with exponential notation.
Frequently Asked Questions (FAQ)
Q1: Why is it important to convert to scientific notation before calculation?
A1: Converting to scientific notation simplifies the calculation by separating the coefficients and exponents. This makes it easier to handle the numerical operations (division in this case) and the manipulation of powers of 10. It reduces the chance of errors when dealing with very large or very small numbers.
Q2: What if the order of operations were different?
A2: If the calculation were 0.10 / (7.2 x 10⁻⁴), the parentheses would dictate that the multiplication (7.2 x 10⁻⁴) should be performed before the division. This would alter the final answer significantly. It highlights the importance of correctly interpreting and applying the order of operations.
Q3: How do I handle more complex calculations involving scientific notation?
A3: The same principles apply to more complex calculations. Convert all numbers to scientific notation, separate coefficients and exponents, perform the arithmetic operations, and then combine the results. Remember the rules of exponents for multiplication and division. For addition and subtraction, you need to ensure the exponents are the same before performing the operation on the coefficients.
Q4: What are the common mistakes to avoid when working with scientific notation?
A4: Common mistakes include: incorrectly manipulating exponents, forgetting to consider significant figures, misinterpreting the order of operations, and making errors in basic arithmetic. Careful attention to detail and methodical calculations are essential.
Conclusion
Solving 0.10 / 7.2 x 10⁻⁴ effectively involves a combination of converting to scientific notation, applying the order of operations, manipulating exponents, and considering significant figures. This seemingly straightforward calculation demonstrates fundamental mathematical principles applicable across diverse scientific and engineering fields. By mastering these principles, you will build a robust foundation for handling more advanced calculations and problem-solving scenarios. Remember to break down complex problems into smaller, manageable steps to avoid errors and enhance your understanding. Practice is key to mastering these techniques!
Latest Posts
Latest Posts
-
Ap Bio Unit 3 Frqs
Sep 03, 2025
-
Line Model 8 X 1 2
Sep 03, 2025
-
Dehydrated Duck Feet For Dogs
Sep 03, 2025
-
Rama Raksha Stotram Telugu Pdf
Sep 03, 2025
-
Labeled Map Of Ancient China
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about 0.10 / 7.2 X 10-4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.