Y Mx B Word Problems
instantreferrals
Sep 15, 2025 · 8 min read
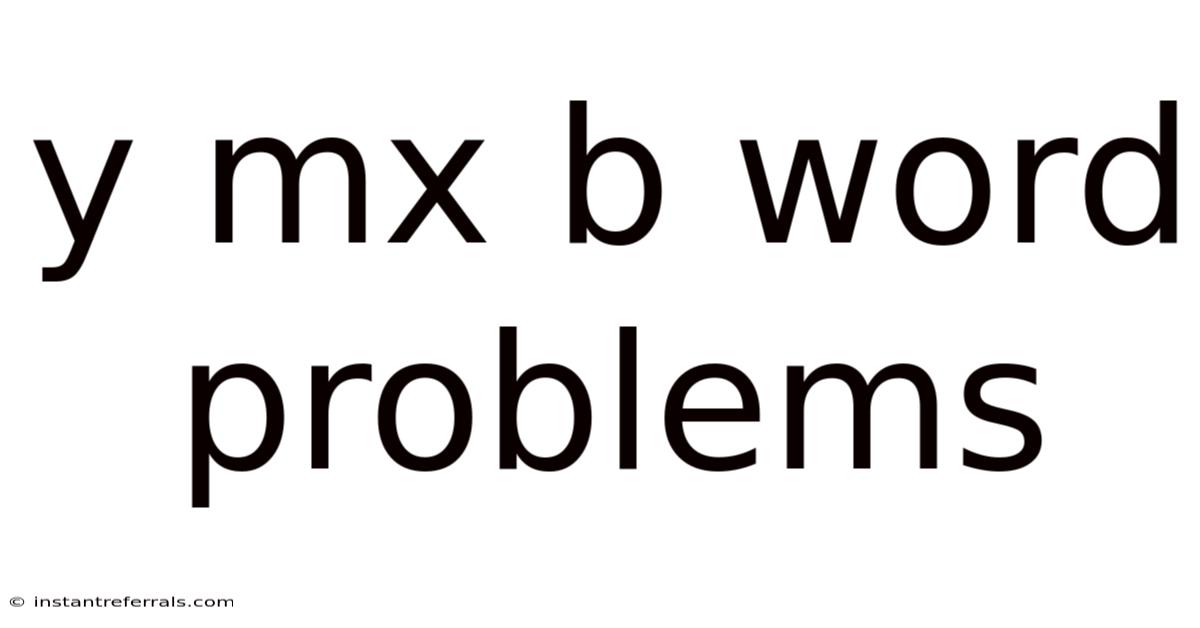
Table of Contents
Mastering the Slope-Intercept Form: Solving Word Problems with y = mx + b
The equation y = mx + b, also known as the slope-intercept form, is a fundamental concept in algebra. Understanding this equation is crucial for solving a wide range of real-world problems, from calculating the cost of a taxi ride to predicting the growth of a population. This article provides a comprehensive guide to understanding and applying y = mx + b to solve word problems, equipping you with the skills to confidently tackle such challenges. We'll explore various scenarios, offering step-by-step solutions and insightful explanations.
Understanding the Components of y = mx + b
Before diving into word problems, let's solidify our understanding of the equation itself. Each component plays a vital role:
-
y: Represents the dependent variable. This is the value that changes based on the value of x. Think of it as the outcome or result.
-
m: Represents the slope, which indicates the rate of change. It describes how much y changes for every unit change in x. A positive slope means an increasing relationship, while a negative slope means a decreasing relationship.
-
x: Represents the independent variable. This is the value that you can change or control. It's the input that influences the outcome.
-
b: Represents the y-intercept. This is the value of y when x is zero. It's the starting point or initial value.
Step-by-Step Approach to Solving Word Problems
Solving word problems involving y = mx + b requires a systematic approach. Here's a step-by-step guide:
-
Identify the Variables: Carefully read the problem and identify the dependent variable (y) and the independent variable (x). What is being measured or calculated? What is influencing that measurement?
-
Determine the Slope (m): Look for information describing the rate of change. This might be expressed as a rate per unit, a percentage increase or decrease, or a similar indicator. The slope represents this rate.
-
Find the y-intercept (b): Identify the initial value or the value of y when x is zero. This is often stated explicitly in the problem or can be inferred from the context.
-
Write the Equation: Substitute the values of m and b into the equation y = mx + b.
-
Solve the Problem: Use the equation to answer the question posed in the word problem. This might involve substituting a value for x to find y, or vice-versa, or solving for a specific point on the line.
Example Word Problems and Solutions
Let's work through several examples to illustrate the process:
Example 1: Taxi Fare
A taxi charges a flat fee of $3 plus $2 per mile. Write an equation to represent the total cost (y) based on the number of miles (x). What is the cost of a 5-mile taxi ride?
Solution:
-
Variables: y = total cost; x = number of miles.
-
Slope (m): The cost increases by $2 per mile, so m = 2.
-
y-intercept (b): The flat fee is $3, so b = 3.
-
Equation: y = 2x + 3
-
Solution: To find the cost of a 5-mile ride, substitute x = 5 into the equation: y = 2(5) + 3 = 13. The cost is $13.
Example 2: Phone Plan
A cell phone plan costs $20 per month plus $0.10 per text message. Write an equation to represent the total monthly cost (y) based on the number of text messages (x). How many text messages can you send if your monthly budget is $35?
Solution:
-
Variables: y = total monthly cost; x = number of text messages.
-
Slope (m): The cost increases by $0.10 per text message, so m = 0.10.
-
y-intercept (b): The base monthly cost is $20, so b = 20.
-
Equation: y = 0.10x + 20
-
Solution: To find the number of text messages for a $35 budget, substitute y = 35 into the equation and solve for x: 35 = 0.10x + 20; 15 = 0.10x; x = 150. You can send 150 text messages.
Example 3: Plant Growth
A plant grows 1 inch per week. It was initially 2 inches tall. Write an equation representing the plant's height (y) after a certain number of weeks (x). How tall will the plant be after 8 weeks?
Solution:
-
Variables: y = plant height; x = number of weeks.
-
Slope (m): The plant grows 1 inch per week, so m = 1.
-
y-intercept (b): The initial height is 2 inches, so b = 2.
-
Equation: y = x + 2
-
Solution: To find the height after 8 weeks, substitute x = 8 into the equation: y = 8 + 2 = 10. The plant will be 10 inches tall.
Example 4: Depreciation
A car depreciates in value by $2,000 per year. It was initially worth $20,000. Write an equation to represent the car's value (y) after a certain number of years (x). What will be the car's value after 3 years?
Solution:
-
Variables: y = car value; x = number of years.
-
Slope (m): The car depreciates by $2,000 per year, so m = -2000 (negative because the value decreases).
-
y-intercept (b): The initial value is $20,000, so b = 20000.
-
Equation: y = -2000x + 20000
-
Solution: To find the value after 3 years, substitute x = 3 into the equation: y = -2000(3) + 20000 = 14000. The car will be worth $14,000.
Example 5: Savings Account
You deposit $1000 into a savings account that earns 5% interest per year. Write an equation to represent the balance (y) in the account after a certain number of years (x), assuming no additional deposits or withdrawals. What will be the balance after 5 years? (Note: This example involves exponential growth, but we can approximate it linearly for a shorter time frame.)
Solution: (Linear Approximation)
-
Variables: y = account balance; x = number of years.
-
Slope (m): The account earns 5% interest per year, so the balance increases by 0.05 * 1000 = $50 per year. Therefore, m = 50.
-
y-intercept (b): The initial deposit is $1000, so b = 1000.
-
Equation: y = 50x + 1000
-
Solution: To find the balance after 5 years, substitute x = 5 into the equation: y = 50(5) + 1000 = 1250. The approximate balance after 5 years is $1250. (Note: The actual balance would be slightly higher due to the compounding effect of interest.)
Dealing with More Complex Scenarios
While the examples above showcase straightforward applications, word problems can become more complex. You might encounter situations requiring:
-
Multiple steps: The problem may require solving for one variable before substituting it into another equation.
-
Systems of equations: Some problems might involve two or more related equations that need to be solved simultaneously.
-
Interpreting graphs: You might be presented with a graph representing the relationship between x and y, and asked to interpret the slope, y-intercept, and other relevant information.
Remember to always carefully read the problem, define your variables, and systematically apply the principles of the y = mx + b equation. Practice is key to mastering this essential algebraic skill.
Frequently Asked Questions (FAQ)
Q: What if the problem doesn't explicitly state the slope or y-intercept?
A: In such cases, you'll need to carefully analyze the information provided to infer the values of m and b. Look for clues that indicate the rate of change (slope) and the initial value (y-intercept). Sometimes, you might be given two points on the line, from which you can calculate the slope using the formula: m = (y2 - y1) / (x2 - x1).
Q: How do I handle word problems involving negative slopes?
A: Negative slopes simply indicate a decreasing relationship between x and y. For example, if a quantity is decreasing at a certain rate, the slope will be negative. Remember to include the negative sign when writing the equation.
Q: What if the relationship isn't perfectly linear?
A: The y = mx + b equation is best suited for linear relationships, where the rate of change is constant. If the relationship is non-linear (e.g., exponential growth or decay), a more complex equation will be needed. However, for short time periods, linear approximations can sometimes be useful.
Q: Can I use a calculator or graphing software to help me solve these problems?
A: Yes! Calculators and graphing software can be valuable tools for solving equations and visualizing relationships. However, it's important to understand the underlying concepts before relying heavily on technology.
Conclusion
Mastering the ability to solve word problems using the slope-intercept form (y = mx + b) is a cornerstone of algebraic proficiency. By following a systematic approach and understanding the meaning of each component of the equation, you can confidently tackle a wide range of real-world applications. Practice is key to building your skills and developing intuition for interpreting these types of problems. With consistent effort, you'll find yourself effortlessly translating word problems into mathematical equations and finding the solutions you need. Remember to break down each problem into manageable steps, and don't hesitate to review the fundamental concepts whenever necessary. Your success in algebra, and beyond, depends on a solid grasp of these foundational principles.
Latest Posts
Latest Posts
-
Properties Of Water Worksheet Answers
Sep 15, 2025
-
Crazy Train Marching Band Pdf
Sep 15, 2025
-
Tropical Rainforest Food Web Producers
Sep 15, 2025
-
Is Christianity Universalizing Or Ethnic
Sep 15, 2025
-
Jasamarbir Arora American High School
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Y Mx B Word Problems . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.